Dimensionality reduction for tumor PDEs

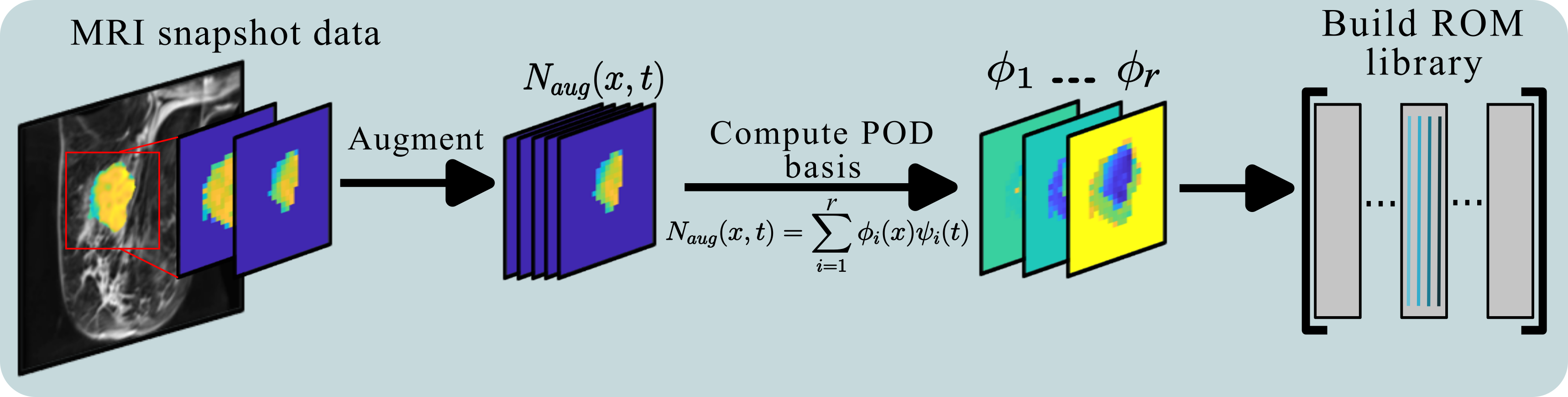
One of the critical components of the research in my dissertation advisor’s lab is numerical modeling in three dimensions, based on high resolution imaging data. While these simulations can provide accurate depictions of tumor growth and response, the models themselves require significant computational resources, whether HPC or time, to fit and use. In this project we desired a reduced order model that could capture the same mechanisms with a fraction of the cost.

Using orthogonal projections, we can place the full resolution PDE into a low dimensional space for evaluations of the model. These projections are based directly on the measured data from an individual patient, and allow for reductions in both the state and parameter spaces. A library built with the projections allows for fast interpolation across the parameter space, replacing operator builds at each step during a model fit. For a relatively low cost to build the reduced model and library, simulation and calibration speeds decrease by up to three orders of magnitude with the framework. This allows for near instantaneous calibration and simulations of the model on almost any PC.

The full publication, Fast model calibration for predicting the response of breast cancer to chemotherapy using proper orthogonal decomposition, is available here

Check out the GitHub! Examples for building and running the reduced model are available in MATLAB using artificial data. This framework can easily be adapted for variations in response terms.